

|
Spoilers ahead! - This page contains the answers to the puzzle. If you haven't already come up with your own answers, you're in the wrong place. Please see the description of the Four Dogs Puzzle first, think about it, and then read this page! |
|
So all dogs start off at the same time, with A chasing B, B chasing C, C chasing D and D chasing A. One possible first thought is that they don't ever meet up, they just chase each other round in circles. However, a quick analysis shows that that's not right. They would only go round in circles if they started off running at a tangent to the centre, but they start off towards the adjacent corner of the square. If you think about components of velocity, there is a part of each dog's motion at a tangent, but also a radial component towards the centre. Therefore the dogs get closer together, you can quickly see this with a practical demonstration.
Let's look at dog A in the picture. Starting off in the south-east corner of our square, it starts travelling due North towards dog B. At the same time, B starts moving due West, and because A is chasing B, the path of A must bend from due North round to the left as it goes. B's path, of course, is also bending from West as it follows C, and also bends round to the left. From the symmetry of the problem, you can see that the paths of each of the dogs must be identical, the curves are just rotated. So all the dogs spiral inward towards the centre of the room. Note that we still don't know whether they ever meet or not, but we know that the general form is a spiral, not a circle.
We can also see by the symmetry of the problem, that if the dogs do meet, then they all meet together (all the dogs are equivalent, so we couldn't have two dogs meeting in one place and the other two meeting somewhere else, for example). And the meeting point must be equivalent for all four dogs, so it couldn't be in one corner of the room or out towards one of the walls - in fact the only point that's the same for all four dogs is the centre of the room, so if they do meet, they must meet exactly in the centre.
Instead of calculating the distance between two dogs, let's just concentrate on one dog and look at its distance from the centre of the room. After all, we have seen that if the dogs meet, they must meet in the centre because of the exact four-way symmetry.
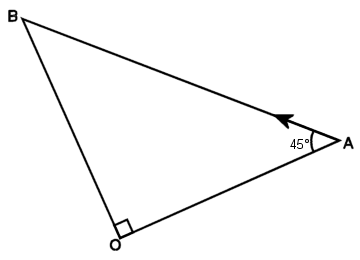
In this diagram you can see that when A runs directly towards B (which it always does), it is running at 45 degrees to the centre of the room O. So we can effectively ignore B and concentrate on the distance from A to O and how that changes. Just considering the components of the dog's velocity, we can see that it has a component cos(45°) towards the centre O and a component sin(45°) in a tangential direction. This component towards O is what is reducing the distance OA.
This means that while the dog is running at an angle of 45 degrees, if it runs a distance d, it will get closer to O by a distance d.cos(45°). Or looking at it another way, in order to get 1 metre closer to O, it actually needs to run for 1/cos(45°) metres. (Numerically, cos(45°) is 1/squareroot(2), so the dog needs to run about 1.41m to get 1m closer to O).
All the dogs start at the corners of the square of side L, so each dog is initially L.cos(45°) from O. So in order to reach the centre of the room, each dog must run for 1/cos(45°) times this distance, which is L, the length of the side of the room. Interestingly, this is the initial distance between each of the dogs, so it's the same distance A would have to run if B never moved and A just ran straight towards B!
Let's look at the problem again, breaking it up into several linear steps (rather than the curves we know it really produces). Then we can make more and more linear steps until we approximate the real curve. We'll start by letting each dog run halfway towards where the next dog is, with their eyes closed so they don't know that the next dog is also moving during this time. Then they'll each open their eyes, see where the next dog is now, and run halfway towards that point, again with their eyes closed.
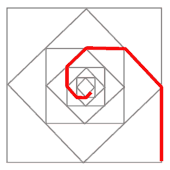
It should be easy to see that each time the dogs open their eyes, all four dogs are again arranged symmetrically in a square, but in a square which is rotated from the one before (in this example each one is rotated by 45 degrees), and each square is also smaller than the one before. So each time they run with their eyes closed, they repeat the same pattern as last time, only rotated and smaller.
So how many steps do we need in this case before the dog reaches the centre of the room? Well, because each dog is only running halfway
towards the next dog each time, we've got the famous Zeno's paradox, they will never meet in a finite number of steps. So does
that mean the dogs will never meet? Not necessarily. We can calculate the total distance run by each dog in this example (remembering
that it will be a different answer to the real problem because they've got their eyes closed). The first stage is simply L/2,
half the length of the wall, and the second step is the same but shrunk by a factor 1/squareroot(2). The third stage is shrunk by a
further factor 1/squareroot(2) and so on, so the sum is a geometrical progression with a final total sum of
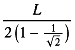 .
.
So, although we know this isn't the exact solution, because they're all running with their eyes closed for most of the time, we can see that the dogs spiral inwards, and do travel a finite distance before meeting at the centre (although they do run an infinite number of steps). Now let's make it a bit closer to the real curve, by only letting the dogs run one third of the way to the next dog before opening their eyes.

We can see that the curve is still of the same form, still with an infinite number of steps, and we can calculate the total distance
travelled in the same way: 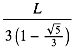 . So now the distance
is only 1.3 times L instead of 1.7 times L for the halfway case.
. So now the distance
is only 1.3 times L instead of 1.7 times L for the halfway case.
Now we can generalise it using shorter and shorter steps. Instead of splitting the distances into 2, or 3, we'll split it into n sections, so each dog will run one nth of the distance towards the next dog with its eyes closed. Once we've calculated that, we just increase n until it's so large that we'll have the curve we want.
Using the same calculations as before, the first section run by our dog is L/n, and the following section is
smaller by a factor given by the triangle of 1/n and (n-1)/n). So the total distance is given by the same
geometric progression, as 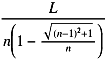 ,
which we can verify gives the same answers as before for n=2 and 3.
,
which we can verify gives the same answers as before for n=2 and 3.
Now we let n grow to some very large value, and see what the distance tends towards. As n gets larger,
any term in n2 will become overwhelmingly large, so (n-1)2+1 can be very well approximated by
(n-1)2, and the denominator becomes (n - (n-1)). So as n tends towards an infinitely
large number, and the dogs follow their curved paths, the total distance run by each dog becomes L.
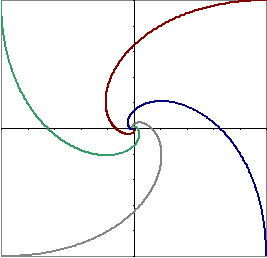
For a visual representation, we can approximate the paths by taking small steps and calculating the positions on a graph, as shown. As we established originally, the forms are symmetric spirals, tightening up as they get closer to the centre. When the dogs are far apart, the angle subtended by the chased dog's movement is small, so the radius of curvature of the paths is large (the paths only bend a bit). As the dogs get nearer, the movement of the dog being chased has a much greater effect on the direction the chasing dog must run, so the radius of curvature gets smaller, and the paths wind in tighter.
In the iterations we did, each square was rotated by a fixed angle and shrunk by a fixed factor at each step. That means that the length of each step decreases exponentially as the angle rotates. Because the radius (the distance from the dog to the centre) is proportional to the step length, that means that as the angle is swept around, the radius decreases exponentially also. This is why these spirals are called "logarithmic spirals" (see the links below). However, this doesn't mean that our dogs approach the centre logarithmically! If our dogs run at a steady speed, the angle is not swept around at a constant rate, it accelerates, keeping the radius decreasing at a linear rate as the dogs run. That's how our dogs can reach the centre and not just asymptotically approach it.
Once we know that the radius decreases exponentially with angle, we can use a general formula to describe the curve using polar coordinates. We can say quite generally that r = ae-bθ where r is the radius (the distance from the dog to the centre), θ is the angle turned through (measured in radians), and a and b are unknown (positive) constants.
The value a determines the size of the spiral, that is if a is twice as big, the spiral looks the same but twice as big. We can fix the value of a by measuring θ from the initial position, so when θ is zero, the radius r is the initial radius, which we can call r0 - we know that the dog is initially in the corner of the room, so r0 is actually L/squareroot(2).
The value b determines how tightly-wound the spiral is, that is whether it loops leisurely round the centre without getting much closer to the centre (for small b), or whether it dives more directly towards the centre (for large b). We can calculate our value of b by looking at the angle between the curve and a radial line from the centre. For our four dogs, they all run at an angle of 45 degrees from the centre, as we saw in the simple expression earlier. This means that dr/dθ is the tan of this angle, which is 1. From our expression of the curve, we can see that dr/dθ is just -br, which tells us that in our case b = 1.
Now we can write the form of the curve as r = r0e-θ and can calculate the total path length again using this formula. To do this we note that the path length of a small section is given by the change in radius at that point (dr/dθ) multiplied by squareroot(2). And since dr/dθ is now just -r, the total path length is r0squareroot(2) times the total integral of e-θ from θ=0 to infinity. This integral is of course just 1, so the total path length is r0squareroot(2), which is L.
Once you've solved the puzzle, it should be straightforward to generalize the answer. Instead of a square room with four dogs, suppose we have a regular polygon with n sides (each still of length L), with n dogs at the corners. How far does each dog travel now? Or ask another question - we know that each dog runs a finite distance before it reaches the centre. But how many revolutions does each dog make, that is how many times does each dog go around the centre? After one revolution, how far is the dog from the centre compared to the distance at the start?
A brief but authoritative explanation is given by wolfram under the title of "Mice Problem". This discusses the "logarithmic spirals" behind the problem and includes some nice animations of some polygonal variations on the square room. The wikipedia also has a good article on logarithmic spirals and how they can form in nature.
Former maths teacher Susie Lanier has an alternative (although not quite thoroughly explained) solution to this problem, giving the final answer as L.pi/2 instead of L. This answer seems to be based on the assumption that the dogs follow a circular arc to the centre of the square, which from the analysis given here is not the case.
Slightly off-topic, but interesting - a crop circle in Desenberg, Germany was discovered in August 2001 with a pattern strikingly similar
to the sketches shown here. See invisiblecircle.org or
fgk.org for pictures.
Whether a quartet of dogs was involved in the formation of this object is not currently known.
Please feel free to submit your thoughts on this problem via email to mail@activityworkshop.net.